Placing 4 Circles on a sphere

Question

I am wondering how I can create a sphere with 4 equally spaced, equally sized circles on a ball, similar to the circles in this image:

I only request to know how the positions of these circles are found, and how to create simple circles on each position of a basic sphere.

Thanks in advance :D

Answer 1

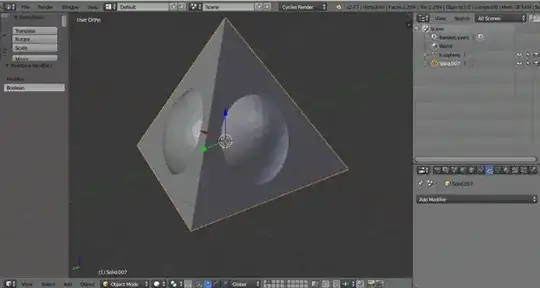
Facected regular solid & boolean op.

Fastest way to find out how to sudbidive the 3D space of the sphere in n parts without relying on complicated solid-angle formulas is to use regular solids.

The idea behind this is to think about the sphere as only an "external shell" that defines a boundary; what we really care is to subdivide the space itself. Regular solids, because the way they are built, already have this property.

The operator can be found in the Extra Objects add-on, which is not enabled by default, but it comes boundled in with the official build.

As you would like to subdivide the sphere in 4 parts, what we are looking for is the Tetrahedron:

By simply scaling the solid, you can adjust the radius of the circles upon the sphere. At the moment there is no geometry on the common edge. In order to make the intersection real, we should also perform some kind of boolean operations.

In this example I added and apply an Intercept boolean modifier, than select the boundary edge loops with Select edge loop (Alt+MouseDx) and finished by running the Separate command.

Answer 2

Another approach also based on the tetrahedron but which does not use the boolean modifier in order to obtain a regular mesh at the end.

• Add a tetrahedron
• Add a circle : the circle needs to have a amount of vertices which is a multiple of 3, because each circle could be connected to 3 others (for instance 36 vertices)
• Parent the circle to the tetrahedron (select the circle and the tetrahedron in this order, then Ctrl+P) and make the circle dupliverts, with orientation checked

• Now align the circle to the Y axis in edit mode so that the dupliverts are aligned to the vertices normals

Once done, first you can refine the circle in order to prepare its geometry. For instance this :

After that, add a sphere and give it some subsurface (as will use a modifier which needs it, see below).

• Scale the sphere close to the circles perimeters.
• Make the duplicates real (this part is in the note at the end, below), single user and join them
• Add a shrinkwrap modifier a set it to the sphere

Now concerning the amount of vertices for the circles, that allow to have an alignment, so that the circles can be joined regularly :

Note, to make duplicate real and single user : - Select the parent object in object mode - Go to the object/apply/make duplicates real (or Ctrl+Shift+A) - And to make them simple user object/make single user/object & data (then validate "selected")

Edit : a finalized symmetrical sphere based on the four initial circles :