1

I'm trying to create a single procedural palm frond branch with geometry nodes

enter image description here

I would like to instance mesh geometry (leaves) from a collection and stagger them along a spline so they are offset from one another and are roughly 180 degrees opposite each other.

So my question is how to stagger geometry along a spline to create a procedural palm frond branch?

Chris
  • 59,454
  • 6
  • 30
  • 84
Zero Dean
  • 159
  • 9
  • Hi Zero, next time, please add images directly into your question, not links. First links can be broken, then often your question gets useless. Second the reader don't have to follow links to understand your question but can directly see whats happening. thx. – Chris Sep 06 '22 at 02:51

2 Answers2

3

While @Chris' answer is a good direction, it only partially answers your question.

Since I know your concern a bit more, I couldn't help but write an answer to it as well.

I really tried to keep it as lean as possible this time.

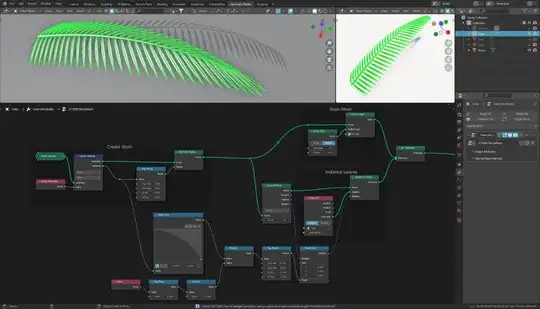
enter image description here enter image description here

First I capture the Spline Factor on the points of the curve.

I then map this with Map Range to a specific range, which I set as the radius for the curve points. These radii serve me later to let the stem become thinner towards the end.

I also use the same factor to define the rotation, because towards the tip the leaves should be more rotated.

With Curve to Points I define the resolution of the curve. At the resulting points the leaves are instantiated.

With the node Float Curve I create a soft curve, which serves me as a basis for the rotation.

But to make sure that every second leaf is rotated in the opposite direction at every second point, I use the index of the points together with the math node Ping-Pong to create a variation. You can also use the Math-Node Modulo here instead.

With this, each point now alternately gives me $0$ or $1$. If I subtract $0.5$ from this, I have the alternating values $-0.5$ and $0.5$, which I multiply with the factor driven values of the Float Curve. I can then use the node Map Range to bring the obtained values into another number range. As values for To Min and To Max I use angles (In Radians!).

As basis for the rotation I use the value Rotation which I get from the node Curve to Points. This rotation lets the leaves follow the stem.

If I now add the previously created angles to this rotation with Rotate Euler, exactly the rotation is created that is needed for the instantiation.


(Blender 3.1+)

quellenform
  • 35,177
  • 10
  • 50
  • 133
  • 1
    Ahhhh, thank you. The blend file is amazing & appreciated and the explanation is especially appreciated here as that was a big part of the puzzle I was hoping to find a solution to. I will experiment with this file and get back to you about my results later. – Zero Dean Sep 07 '22 at 18:34
  • I've been playing with this. I managed to figure out where to add a "trim curve" in order to restrict where the leaves begin on the stalk. And also a "realize instances" at the end so I can collapse the modifiers and end up with an editable mesh. I also figured out how to randomly grab leaves from a collection!

    One thing I haven't been able to figure out is why any leaves I instance lose their texture when instanced. The leaves I instance have UVs and a texture and show up properly in the viewport by themselves...

     – Zero Dean Sep 07 '22 at 21:34
1

you can use this node setup:

enter image description here

to get this:

enter image description here

to use a collection, just replace my lower arc node by a collection node and check "pick instance" on the instance on points node.

Chris
  • 59,454
  • 6
  • 30
  • 84
  • Thanks so much for the response. I went through the node group and changed the lower arc to a collection, as you suggested. And it works (for my needs) to a degree and it's definitely a good teaching tool. One thing I had trouble with is while one side of the stem's leaves can be manipulated, I couldn't find a way to manipulate the opposing side (which is likely my lack of experience with geonodes). It may be how I asked the question, but I was hoping for a bit more insight into how to actually offset the leaves, as I am (was) unfamiliar with the mechanism to do so. Thank you. – Zero Dean Sep 07 '22 at 18:28