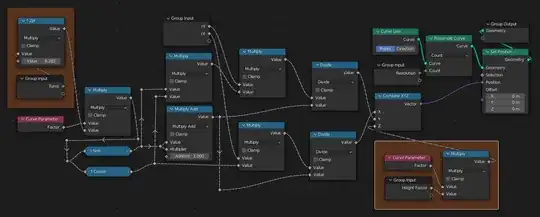
I would like to create a lemniscate, which is a figure 8. I would like it to rise as it swoops back and forth. I tried to do model the 2-d version using polar coordinates [r^2=(a^2)cos(2theta)] or rectangular/cartesian [(x^2+y^2)^2=(a^2)*(x^2-y^2)], but couldn't figure out how.
So, I tried to do a workaround using arcs. I was able to make two arcs and join them, then put in a little bit of height. However, there is a gap between the two arcs/curves. This occurs where the first curve ends and the second begins. How can I join them so there is no gap (i.e., so it is one long curve)? Then, how can I turn that into an array?
If anyone does also know a workaround on the polar plotting, that would also be hugely appreciated!