7

I am having trouble understanding the affine gap penalty in the following example -

enter image description here enter image description here enter image description here

I am not sure where the 3 and 4 come from or the 4 and 5 in cells 1,3 and 2,4. I'm not understanding how the affine gap penalty works here. I understand how the linear gap penalty worked in the Needlemen_Wunsch but not this.

H5159
  • 173
  • 4

2 Answers2

5

The linear gap penalty has a cost which is directly proportional to the length of the gap: the gap costs 1 unit per consecutive missing base.
The simplest case is assigning each unit (= each missing base) a penalty of 1:

g(k) = k

Or more generally, if you want to increase the penalty per base to 2, 3 or n:

g(k) = n * k
with k = length of the gap, and n = cost of 1 missing base

The affine gap penalty has a cost that follows -as its name conveniently states- an affine function.
The idea behind it, is that any gap in an alignment has a cost with two components:

  • the "gap opening" penalty: it is a cost payed only once per gap, basically just for existing.
  • the "gap extension" penalty: equivalent to the linear gap penalty, it costs 1 unit for each consecutive missing base.

The general formula for the cost is then:

g(k) = a + n*k
with a= opening penalty, n= extension penalty, k= length of the gap

Compared to the linear gap penalty, this will give a small bonus to longer consecutive gaps compared to skipping one nucleotide, matching one, skipping one again etc (because in the case of longer gaps, you only pay the opening penalty once, so the global cost per base decreases).

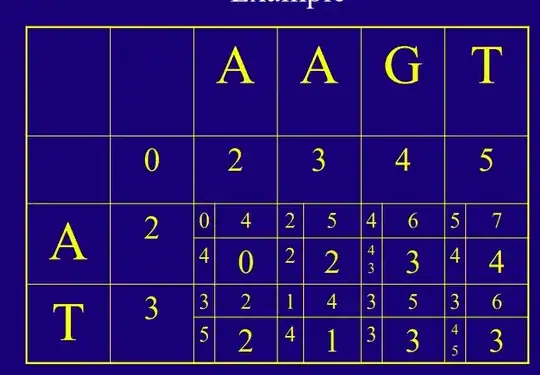
Cells on your diagram:
From what I understand, you're working with an affine penalty of g(k) = 1 + 1*k. For the [3,4] you're "coming" from the score of 2 on the left (cell 1,2). You either:

  • match the A (row 1) with G (column 3) and get a penalty of 1 for substitution -> total of previous 2 + new 1 = 3
  • open a gap to skip the G (column 3) and get a penalty of 2 (1 for opening + 1 because gap length of 1) -> total of previous 2 + new 2 = 4.

So you choose the lesser penalty and go with 3, which is the number selected in the bigger box.
The explanation is the exact same one for the other cell you mentioned.

Kerkyra
  • 186
  • 3
  • I believe I understand now. The reason why we can get 3 or 4 is because in the previous cell, the optimal score of 2 could have come from either the left or the diagonal. If it had come from the diagonal, we are starting a new gap and thus we get 2 + (1 + 1) = 4. However, if we come from the left, we are simply adding to the already existing gap so we get 2 + 1 = 3. Is this the correct way to think about it? – H5159 Oct 03 '17 at 15:58
2

The formula your slide shows describes a dynamic programming with a general gap cost. Finding the optimal solution takes $O(n^3)$ time. No one is using the algorithm these days. This is the first time I see an attempt to fill a matrix with this algorithm. It is interesting, but I am not sure how it works. Although affine gap cost is a special case of general gap cost, the algorithm to find the best score is very different, so is the time complexity. With modern affine gap formulations, each cell holds three values:

  1. The overall optimal score (or the optimal score if this cell is a match, which yields an equivalent but different formulation)
  2. The optimal score when the cell ends at a deletion
  3. The optimal score when the cell ends at an insertion

The values in each cell only depends on the up, left and up-left cells in the matrix. You fill the matrix from the top left corner to the bottom right. This is an $O(n^2)$ algorithm, because you traverse each cell once. For more details, you can read this note. I would recommend to learn affine gap cost the normal way.

user172818
  • 6,515
  • 2
  • 13
  • 29
  • which algorithms produce local alignments under $O(n^3)$? Are there any R implementations of such algorithms? – Vass Sep 06 '20 at 02:02