5

The BioPython documentation shows the following:

11.6.3 Measuring torsion angles Use the vector representation of the atomic coordinates, and the calc dihedral function from the Vector module:

>>> vector1 = atom1.get_vector()
>>> vector2 = atom2.get_vector()
>>> vector3 = atom3.get_vector()
>>> vector4 = atom4.get_vector()
>>> angle = calc_dihedral(vector1, vector2, vector3, vector4)

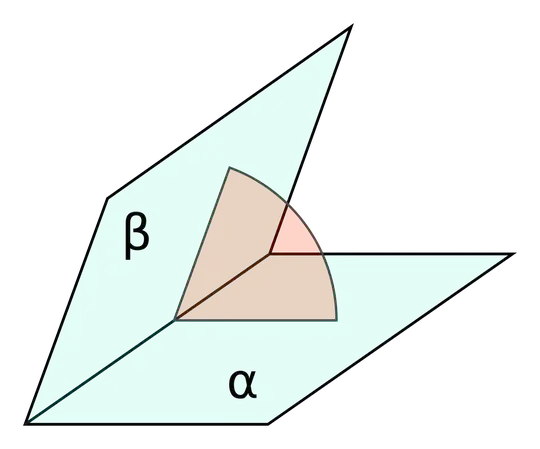
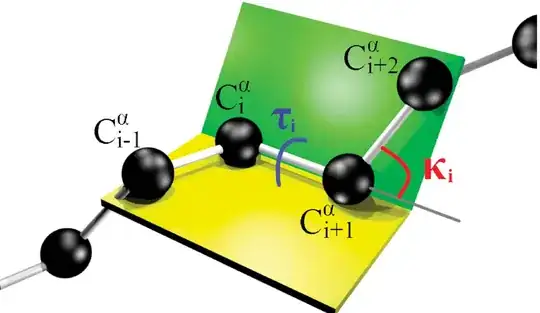
We know that a torsion angle between N-C-alpha and C-alpha-C planes.

So, the minimum number of points required to form a plane is 3.

Then, Why does BioPython require 4 vectors?

user366312
  • 654
  • 2
  • 14
  • 1
    If you want to check out the actual source code to clarify this further see https://docs.python.org/3/library/inspect.html#inspect.getsource —a handy function in a great package. – Matteo Ferla Oct 11 '21 at 08:44
  • You say you need two planes and that you can describe each plane with three points. That's 6 points total, which in three-dimensional space require 18 coordinates. Four vectors require only 12 coordinates. What is there to complain about? –  Oct 10 '21 at 21:12
  • Vector spaces include the origin, by definition. The origin supplies two of the six points need to define the two planes. – merv Oct 12 '21 at 17:56

2 Answers2

5

From wikipedia on torsion angles:

A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common.

Two sets of three with two in common makes four total atoms.

You are defining not one plane but two half-planes or planes.

Wikipedia includes the following as an illustrative image:

Angle between two half-planes (α, β, green) in a third plane (pink) which cuts the line of intersection at right angles "Angle between two half-planes (α, β, green) in a third plane (pink) which cuts the line of intersection at right angles"

In this image I interpret the atoms to be at the vertices of the planes, e.g. the two atoms that are in common between the two planes are those at the points of intersection of the planes, and the two other atoms extend the planes $\alpha$ and $\beta$.

Maximilian Press
  • 3,989
  • 7
  • 23
4

To compute dihedral angles you require 4 atoms and hence for vectors to determine two planes (see this figure here) whose angle you want to measure - dihedral angle.

You can also check Fig 55 from the GROMACS documentation

https://manual.gromacs.org/documentation/current/reference-manual/analysis/bond-angle-dihedral.html

Definition of (virtual) Cα backbone bond (κ) and torsion (τ) angles. from https://journals.plos.org/plosone/article/figure?id=10.1371/journal.pone.0215141.g002 from https://journals.plos.org/plosone/article/figure?id=10.1371/journal.pone.0215141.g002