What is the shape of orbit assuming gravity does not depend on distance?

Question

We know that the orbit of the earth is elliptical considering the force of gravity is inversely proportional to the square of the distance. But assume that, gravity does not depend on distance. Considering that situation, what will be the shape of the orbit? Will it be elliptical, circular, hyperbolic or what?

Answer 1

Circular orbits are always possible for any central force law, but noncircular orbits would resemble rosettes. Here's a specific example for the case where the force is constant with distance:

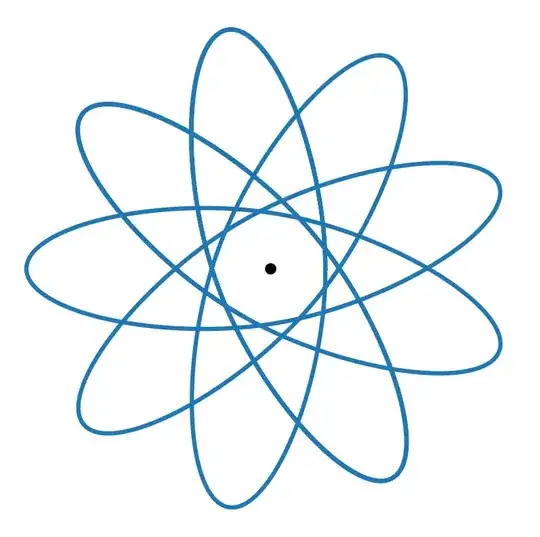
By chance, I selected parameters that happen to make a (at least approximately) closed orbit. That won't happen in general. When I change the angular momentum slightly, I get the following. 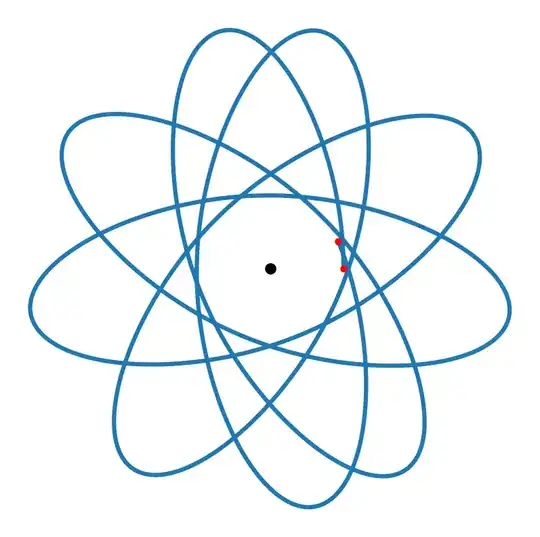Here the red points show the starting and ending positions of the orbiting object. The positions and velocities don't quite match up, and if I continue the orbit indefinitely, it fills up the entire annulus between the minimum and maximum radii:

Click here for an animation.

These kinds of orbits are common in galactic contexts, where things are orbiting inside extended mass distributions. The particular case of a force that is constant with distance corresponds to an orbit inside a density distribution that scales inversely with radius, i.e. $\rho\propto r^{-1}$. That's precisely the structure of the deep interior of the Navarro-Frenk-White density profile.

Answer 2

In addition to Sten's great answer, it should be noted that under constant gravity all orbits are bounded. Therefore, there aren't any orbit like the hyperbolic ones mentioned in the question.

That can be seen from the fact that potential energy is unbounded. Every meter a particle moves away from the centre, it gains the same amount of potential energy. Therefore, for whatever kinetic energy the particle may have, there is a maximum distance it can reach even when all its kinetic energy is converted into potential energy.

Additionally, first and third Kepler's law wouldn't hold. However, second Kepler's law would hold, because it's equivalent to the conservation of angular momentum, and angular momentum is always conserved under a central force, no matter its magnitude.

Answer 3

There wouldn't be standard orbits at all.

The Earth orbits the Sun because the Sun's mass dominates the local spacetime. By removing distance from the gravitational equation, the Earth would, with the same magnitude, now be attracted to every other object in the Universe, without the tempering effect of distance. It would be equally attracted to all similarly sized stars, and will be more attracted to larger stars, no matter how far away they are.

Everything would likely disintegrate.

The only reason the Earth is a single item is that its collective mass dominates its local spacetime enough to keep itself together. Without that local dominance, the Earth's internal pressure would blast its component pieces outward.

Answer 4

I agree with the answer of @MichaelRichardson that a constant, i.e. distance-independent, gravitational force throughout the universe would make any structures in it unstable. This follows directly from the The Virial Theorem, which tells us that in general the average kinetic energy $\bar{T}$ is related to the average potential energy $\bar{U}$ by the equation $2\bar{T}=k\bar{U}$ where $k$ is the power index of the interaction potential. For a constant force field we would have $k=1$ ( as $U=\alpha x$). Now if we let $x\rightarrow \infty$ we have in this case $\bar{U}\rightarrow \infty$ and per the Virial Theorem $\bar{T} \rightarrow \infty$. This is obviously not possible without any structure flying apart. In order to have localized structures the potential energy requires a power index $k<0$ (for gravity $k=-1$)

For clarification, with the usual law of gravity ($U=-\alpha /x$), an object is bound when the sum of kinetic energy and potential energy is less than zero ($T+U<0$)). For a circular orbit we have in this case $T=-1/2\cdot U$. For the Earth the orbital velocity $v=\sqrt{2T/m} $ is about $30 km/sec$. The nearest star has about a distance of $3\cdot 10^5 AU$ from the Sun, which would make its orbital velocity $1/\sqrt{3\cdot 10^5}$ times smaller, i.e. it could only move at about $0.05 km/sec$ to stay in orbit. However, stars in our galaxy have typically proper motions of the order of $100 km/sec$, so they are about 3 orders of magnitudes too fast to be bound. This is the reason why our solar system can be treated as a localized structure within but dynamically unrelated to the rest of the galaxy (never mind other galaxies).

Consider in contrast a hypothetical world where masses interact with a constant (distance independent) force of gravity. In this case the required equality between centrifugal and gravitational force would read

$$m\frac{v^2}{r} = const.$$

that is $v \propto{\sqrt{r}}$ . This means the orbital velocity would increase rather than decrease with increasing $r$. The orbital velocity of the star would now be $\sqrt{3\cdot 10^5}\cdot 30 km/sec = 1.6\cdot 10^4 km/sec$. So with such a force law the whole galaxy (and beyond) would be part of our solar system, or rather everything in our universe would be just one big system of randomly moving objects, without any kind of local structures being able to exist at all in the long term.

Of course, these absurd consequences of a hypothetical constant gravitational force not only contradict reality, but are merely the result of a conceptual inconsistency by ignoring that point masses (or masses that can be approximated as such) by definition imply a $1/r^2$ force law. This is because outside the mass distribution, the divergence of the force field must by definition vanish , i.e. (considering only the radial component here)

$$ div(\vec{F})=\frac{1}{r^2}\cdot \frac{\partial}{\partial{r}}(r^2\cdot F) = 0$$

For $F=const$, this would however result in a divergence $\propto{1/r}$ which contradicts the initial assumption that there are no mass sources outside the mass. It is immediately obvious that the above equation is only satisfied for $F=1/r^2$.