15

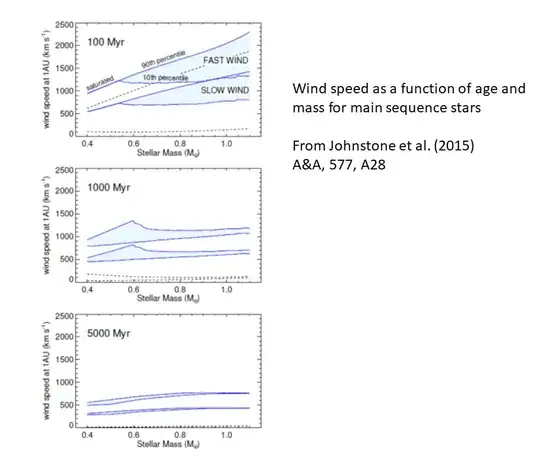
I'm wondering if different stars produce wind at different speeds, and if so, what factors determine that speed.

Per this answer, our star produces wind with a speed between ~250–820 km/s. It seems safe to assume that the wind speed for each star is variable.

This other answer gives the Reimers mass-loss formula, which accounts for loss via radiation and wind, but states that one term must be measured empirically. (And, in any case, I'm interested in wind speed, not mass carried away.)

Wikipedia says we don't have a very good understanding of how the solar wind is accelerated, which suggests it may not be possible to answer this question.

Still, as a layman, it seems like it should be possible to make general predictions about a star's wind, given a few facts about that star, namely: mass, angular velocity, and age.

For example, would a blue star have faster wind because of its higher temperature or (I assume) stronger magnetic activity? Or would it be slower because of its greater gravity? Or would it depend substantially on the star's rotation? Or would all stars have similar wind speeds because of facts about idealized gasses (I'm thinking of Maxwellian distribution)?

Tom
  • 251
  • 1
  • 5

2 Answers2

9

The answer depends very much on what type of star you are talking about and what the driving mechanism of the wind is. Broadly we can split stars up into low-mass main-sequence stars (say $<2 M_\odot$), where the wind is probably thermally driven by gas pressure gradients, high-mass main-sequence and evolved stars, where the wind is driven by radiation pressure, and red giants where the wind is also driven by radiation pressure, but the opacity source is dust.

For low-mass main sequence stars, there are no observations to make an empirical relationship and there are major theoretical uncertainties in estimating a wind velocity. This is discussed by Johnstone et al. (2015a) who find the wind velocity is (at 1 au) $$v = 73.39 + 221.14T_0 - 11.28T_0^2 +0.28T_0^3\ , $$ where $T_0$ is the base temperature of the wind. The main uncertainty is whether the base temperature of the wind is determined by the magnetic fields present (since the corona is ultimately heated by magnetic fields), or whether it is directly connected to the stellar escape velocity. If the former, then the wind speed will be connected with the rotation rate of the star and its spectral type in a very non-linear way. Some plots are presented by Johnstone et al. (2015b) and I reproduce one of these below. The rotation dependence is manifested as an age dependence since these stars spin down as a result of their magnetised winds. This in turn reduces the dynamo-induced magnetic activity and reduces their coronal temperatures.

Johnstone et al. 2015 wind speed

Hot, early-type O and B stars have winds driven by radiation pressure. The theory of "line-driven" winds is complex and cannot be simply summarised in a SE answer. The terminal wind velocity is usually 2-3 times the escape speed at the star's photosphere. But there is a complex detailed dependence of this factor on spectral type and hence luminosity (or mass). The terminal wind speeds are in the range 1000-3000 km/s for B $\rightarrow$ O-stars. This relationship of a few times the escape velocity works reasonably well for Wolf-Rayet and other hot, evolved stars too.

The winds from cool giants are radiatively driven, but this time the opacity source is dust. For these stars, the terminal wind velocity is given approximately by $$ v_{\infty} \simeq \frac{v_{\rm esc}^2}{1000\ {\rm km/s}}\ , $$ which is lower than the escape velocity. Roughly 10 km/s for M-type supergiants, up to 70 km/s for K-type giants. Higher velocities are not found because the dust disintegrates by sputtering once accelerated to these speeds.

ProfRob
  • 151,483
  • 9
  • 359
  • 566
7

All stars, and also planets, lose mass because of atoms escaping from the atmosphere that are faster than the gravitational escape velocity. This suggests already that gravity i.e. the mass of stars is the crucial factor here. The gravitational potential energy of an atom with mass m near the surface of a star with mass M and radius R is of the order

$$E_{pot} =-\frac{GMm}{R}$$

where $G$ is the gravitational constant.

and according to the virial theorem, the associated kinetic energy is

$$E_{kin}=-\frac{E_{pot}}{2}$$

which corresponds to a temperature

$$T=E_{kin}/k$$

where $k$ is the Boltzmann constant.

If you evaluate this for the Sun, you get

$$T=1.1\cdot 10^7 K$$

which corresponds to a thermal speed of hydrogen of

$$v=\sqrt{\frac{2kT}{m}} \approx 400 km/sec$$

This is essentially the solar wind speed we observe.

Given the fact that the radius $R$ in the denominator in the first equation increases with mass as well (depending on the mass-radius relationship) and the square root in the last equation, the dependence of the stellar wind speed on the mass of the star should be fairly weak though.

Of course this would only be an average speed. The fact that we are dealing with charged particles here introduces all kinds of electromagnetic effects that can change the observed speed quite drastically in certain situations.

Thomas
  • 3,061
  • 5
  • 12
  • 7
    I think it would be good to specify that this explanation only may explain the very small mass loss from low-mass stars (e.g. the Sun). The much higher mass loss from high-mass stars is caused by radiation pressure, not thermal escape. – pela May 02 '22 at 09:22
  • 3
    A great textbook for learning about stellar winds is by Lamers and Cassinelli, and here is an abridged version for free with many chapters. They have a great intro on the winds of high mass stars. https://ui.adsabs.harvard.edu/abs/1999isw..book.....L/abstract – Daddy Kropotkin May 02 '22 at 10:36
  • 1
    @pela The OP was asking about the solar wind speed not the mass loss. The two are not necessarily related. If the Sun had a thinner photosphere (i.e. fewer of the particles with 'virial' energy would be stopped due to inelastic collisions with neutrals) the mass loss of the Sun would be much higher but the energy of the solar wind would still be the same, given essentially by the gravitational potential energy i.e. the mass. – Thomas May 02 '22 at 11:43
  • Doesn't the rotational speed of the star contribute to the launch speed of stellar wind particles? – Carl Witthoft May 02 '22 at 12:34
  • 1
    @CarlWitthoft A rotation shouldn't actually make a difference to the consideration above. The virial theorem relates the gravitational potential energy to the total kinetic energy. If the latter contains rotational energy as well, then the thermal energy must be correspondingly less for the whole system to be in equilibrium. Added together, the total kinetic energy and thus the escape speed will still be the same as for a non-rotating star (which the Sun with about 2 km/sec surface speed pretty much is). – Thomas May 02 '22 at 13:58
  • 1
    The OP asks about how to calculate a stellar wind speed based on the parameters of the star. This answer uses a virial calculation that assumes the gas at the surface of the Sun is in a virial equilibrium. The virial theorem cannot be applied to individual components of a system like this. Without non-radiative magnetic heating, the region above the photosphere would be cooler than the photosphere and the Sun's corona is in any case much cooler than $10^7$K on average. – ProfRob May 02 '22 at 14:20
  • 1
    Observationally, it is totally uncertain whether wind velocities for low-mass stars scale with escape velocity (which is essentially what is assumed here) or whether they scale with coronal temperature which in turn depends on the age, rotation rate and mass of the star. High-mass stellar winds are of course radiatively driven and there is no direct connection with any coronal temperature. – ProfRob May 02 '22 at 14:22
  • 1
    Further, the speed of the solar wind is about 400 km/s at the orbit of the Earth, not at a solar radius. – ProfRob May 02 '22 at 15:35
  • @ProfRob You can not use LTE to model the photosphere up to an energy of more than 3 orders of magnitude above the average energy. There will always be a few keV protons and electrons that manage to penetrate the photosphere from below without suffering energy loss due to inelastic collisions with neutrals. Others may only suffer a partial energy loss. And depending on the details of the energy distribution function, the solar wind may appear to speed up after having done work against solar gravity. – Thomas May 02 '22 at 16:20
  • @Thomas Stars as nozzles; how important is thermodynamics and the de Laval nozzle equation for understanding the speed of the solar wind vs distance? – uhoh May 02 '22 at 22:07
  • But my comment would be the same for the speed. It’s just two different mechanisms. – pela May 03 '22 at 08:40
  • @pela Bear in mind that you have only a given gravitational potential energy to start with. If you assume this is converted into thermal energy + additional photon energy, the total energy density should still add up to the same amount as given by the virial theorem. Otherwise you would be violating energy conservation. – Thomas May 03 '22 at 20:47
  • @pela The question is also: how accurate are the figures for stellar wind speeds for stars other than the Sun. As they can obviously not be measured in situ, they can can only be derived indirectly based on certain assumption, and are thus probably not more than estimates. – Thomas May 03 '22 at 21:56
  • You don't need to violate any laws by using different mechanisms to accelerate matter to different speeds. As a counterexample, remember that supernovae eject matter with tens of thousands of km/s. Regarding your second comment, I don't think measurement uncertainties are a problem for the velocity of stellar winds in stars other than the Sun. They can be measured from low-ionization absorption lines in the ejecta, the precision of which is extremely high. Mass-losses may be more uncertain, though (but a definitely much higher than for the Sun and other low-mass stars). – pela May 04 '22 at 08:17
  • @pela Supernovae can't be used as a counter-example here. All arguments here refer to stars that are in some kind of hydrostatic equilibrium i.e. where the gravitational potential energy is balanced by the sum of the kinetic (thermal) energy and the radiative energy associated with it through the Stefan-Boltzmann law. – Thomas May 05 '22 at 16:01