Yes and No. — It depends on what you mean by "stable". To be precise, "stable" means immune to small perturbations. "Equilibrium" can be either "stable" or "unstable," as shown in any first-year Calculus text.
Can you balance a pencil on its point?
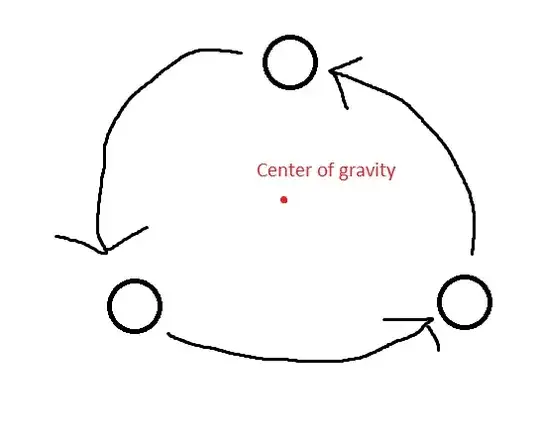
If you have three ideal spherical bodies (and an otherwise empty universe), moving according to Newtonian gravity (or perhaps even Einstein's relativity), and each body is moving exactly at the right velocity, then this system could exist.
However if you perturbed it by even the smallest amount, then it would gradually deviate from this orbit and probably end up with either a collision, or an ejection of one of the planets. In this sense it is not stable.
It is like balancing a pencil on the point. It is possible in theory, but in practice the pencil will always fall down. Similarly, this is possible in theory (or in a computer model) but could not exist in practice.
The best known stable solutions to the three-body problem are hierarchical. Either a "sun" is orbited by a "planet" which is orbited by a "moon", or two "suns" are in a tight orbit, which is orbited by a "planet". In these configurations there is a clear structure, and the orbits of each level can be approximated by Keplerian ellipses.
This solution was found by Lagrange, and it is a special case of the L4 and L5 orbits, in which the three bodies move in an equilateral triangle. Other solutions of the three-body problem are known However non-hierarchical solutions that are not only periodic, but resistant to small perturbations, don't exist when then the three bodies have equal mass.