When talking about celestial bodies orbiting the sun with a decently circular orbit or small aphelion, the heliocentric orbital parameters are almost identical to the barycentric parameters. However, most comet-like (highly eccentric with very large aphelion, but not hyperbolic/parabolic) orbits have vastly different parameters. For instance, according to Wikipedia, the minor planet $2017\ MB_7$ has a heliocentric aphelion of $\sim 7000-9000 \text{ AU}$, while the barycentric aphelion is only $\sim 1800 \text{ AU}$. Why is this happening?
-
quick note: this is the last question asked before graduation (beta logo gone) – WarpPrime Dec 16 '21 at 16:59
-
1Helpful to note that the same article mentions that the barycentric model is based on the long-term change of the solar system barycenter. – WarpPrime Dec 16 '21 at 18:21
-
This is a prime example of a bad wikipedia page. Lots of broken links, lots of personal research based on a misunderstanding of / misuse of osculating elements, it's poorly written; the list goes on and on and on. – David Hammen Dec 17 '21 at 08:27
-
@DavidHammen Do you have a possible explanation for the difference in the barycentric and heliocentric modeling? – WarpPrime Dec 17 '21 at 13:34
-
Using some sort of proper barycentric orbital elements makes sense for objects that always orbit well outside Netptune's orbit -- which 2017 MB7 does not. JPL's Horizon's system uses osculating elements rather than proper elements. That combined with the fact that computing osculating elements from barycentric Cartesian coordinates for objects well inside of Neptune's is more or less garbage in, garbage out. 2017 MB7 was inside Jupiter's orbit at the time of discovery. Using osculating orbital elements based on barycentric position and velocity results in garbage for such an object. – David Hammen Dec 17 '21 at 15:30
-
@David, JPL Horizons uses Chebyshev coefficients fitted to an n-body simulation. https://ipnpr.jpl.nasa.gov/progress_report/42-196/196C.pdf – Greg Miller Dec 21 '21 at 16:36
-
The Wikipedia article doesn't cite a source, and I'm not going to bother actually doing the calculation. But one likely source of confusion is that Kelperian orbital elements are just approximations. An n-body simulation is required to account for the fact that the Sun moves relative to the barycenter. – Greg Miller Dec 21 '21 at 16:44
-
@GregMiller Horizons calculates position and velocity from those Chebyshev coefficients, and then calculates osculating elements from the calculated position and velocity. – David Hammen Dec 21 '21 at 17:56
2 Answers
Inspired by this excellent question,I found this page that describes the issue in some detail for non-specialist readers. If I'm not botching the explanation, the reason for the difference is that near perihelion when the object has its maximum kinetic energy, its potential energy is typically lower relative to the barycenter of the solar system than to the Sun itself. The difference is often enough that highly-eccentric closed orbits about the barycenter appear to be hyperbolic with respect to the Sun, so the difference between aphelions in heliocentric and barycentric coordinates can vary by any amount.
- 1,213
- 2
- 12
- 27
- 3,455
- 11
- 12
-
So which system is typically used before and after perihelion? A lot of comets are said to be hyperbolic but were long-period before perihelion. – WarpPrime Dec 17 '21 at 15:43
-
1@fasterthanlight Neither. The leading ephemerides organizations (JPL in the US, the Institute for Applied Astronomy in Russia, and the IMCCE in France) all calculate their ephemerides by propagating barycentric Cartesian position and velocity. Orbital elements aren't all they are cracked up to be. – David Hammen Dec 17 '21 at 15:50
-
@fasterthanlight - Planetary perturbations near perihelion will change the aphelion for most highly-eccentric objects, regardless of the coordinates used. – antlersoft Dec 17 '21 at 15:51
-
If there were no planets, the Sun would remain at the barycenter, and a small body's orbit would be a perfect Keplerian ellipse. A real trajectory is more complicated. Osculating orbital elements only describe an ellipse which approximates it for the given epoch and center; they are valid for a few months, not years. With that limitation in mind, you can use either barycentric or heliocentric elements to make a short-term prediction of its position. For a long, highly eccentric orbit, elements for an epoch near perihelion are not valid near aphelion.
The Sun's wobble around the barycenter affects other objects' velocities relative to the Sun, leading to significant fluctuations in heliocentric elements when an object is moving slowly. Far from the Sun, barycentric elements are more stable. Close to the Sun, heliocentric elements may fit the real trajectory better.
Here is a plot of 2017 MB7's osculating semimajor axis vs. epoch as estimated by JPL HORIZONS. The barycentric value increases from ~1000 au before 2010 to ~1400 au after 2025 due to a boost from Jupiter. The short-term fluctuations don't necessarily indicate real changes in aphelion, only different parameters for ellipse segments approximating the object's path.
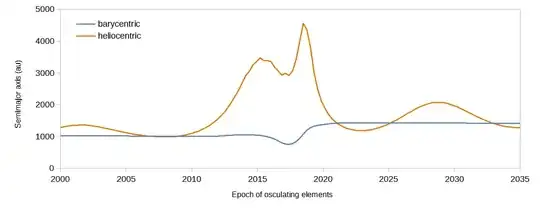
- 18,640
- 1
- 26
- 65
-
Could you explain the (roughly) sinusoidal fluctuations in the barycentric model for the body before and after perihelion? – WarpPrime Dec 24 '21 at 23:31
-
@fasterthanlight In the blue curve, 2017±2 years? You may get a better sense of that by stepping through the JPL orbit viewer. – Mike G Dec 24 '21 at 23:53
-
-
@fasterthanlight The orange curve's smooth ~12-year oscillation outside 2015-2019 is due to Jupiter's effect on the Sun. – Mike G Dec 25 '21 at 03:24