4

If some specific metal is shown in a star's spectrum, does it indicate that the star has that specific metal? For example, the Sun, a G2 star, shows medium strength of Ionised Calcium in its spectrum, but why does the chemical composition of the Sun doesn't really have Ionised Calcium? https://astronomy.swin.edu.au/cosmos/C/Chemical+Composition

Edit: why does the chemical composition of the Sun only have a trace amout of Ionised Calcium, but the strength in the spectrum is not low at all?

Thank you in advance!

Jack the Ranger
  • 1,296
  • 6
  • 24

3 Answers3

4

Surely the sun possesses calcium in its atmosphere, as well as in its bulk volume.

This plot, based on the data published in Asplund et al.,(2009), shows what elements can be found in the solar atmosphere: enter image description here

And we can read off that the abundance [Ca]/[Si] = 0.1 for example. Elements in stellar atmospheres can occur both in absorption and emission in stellar spectra, and of course in their ionized states, when the local temperatures are high enough.

For far-away stars that are observed in the galaxy, foreground contamination of the spectrum may play a role, but this can be removed via doppler-analysis.

AtmosphericPrisonEscape
  • 9,840
  • 1
  • 31
  • 42
  • Hi, I have a little question with the calculation of Ca/Si ratio, as the abundance of calcium is about log5, and log6 for Si, so shouldnt the ratio be 0.89? Thanks. – Jack the Ranger Mar 19 '21 at 14:52
  • 2
    @JacktheRanger: Hi Jack, you have to be careful and observe the little 10 below the log. So a $\rm \Delta log_{10} = -1$ is a factor $10^5/10^6 = 0.1 $ difference in log-10-space. – AtmosphericPrisonEscape Mar 19 '21 at 15:29
  • Ah, I see, I was making a mistake by reading the graph as $\log_{10}^{\text{6}}=$Abundance of Si, but it should be $\log_{10}^{\text{Abundanece of Si}}=6$. Thanks. – Jack the Ranger Mar 20 '21 at 01:54
3

The strength of an absorption feature in the stellar spectrum is dependent on the amount of that element that is in the photosphere but it also depends on the atomic structure of the element and the conditions of temperature and density in the photosphere.

For example the CaII lines need there to be singly ionised calcium ions in the photosphere. This requires a particular range of temperature and density. Too hot and the calcium becomes more ionised; too cool and there are no calcium ions. When the conditions are right, there are two particular transitions in the blue part of the spectrum that have a very high probability of occurring (or a large cross-section if you like) - these are the "H and K" resonance lines. They are called resonance lines because they are transitions from the ground state and often have the twin benefits of a large population of absorbers in the lower (ground) energy state, and a high probability of the transition occurring. There is however also a triplet of transitions in the near infrared that are also very strong, despite arising from an excited state.

There are similar transitions in other elements too, but since Ca is a group II element, singly ionised Ca behaves a bit like neutral atoms of elements in group I. Thus we have equivalent transitions for Sodium (the Na D lines) and for Potassium (in the red part of the spectrum). The Li line is weaker (at 670.8 nm) because there is genuinely much less Li in the photosphere.

There are also absorption lines for Be II and Mg II (singly ionised beryllium and magnesium), but these occur in the UV.

ProfRob
  • 151,483
  • 9
  • 359
  • 566
3

'Absorption' lines are caused by resonance scattering (scattering the radiation out of the line of sight, see illustration below), and resonance scattering has a very large cross section of roughly $10^{-12} cm^2$. This means that even for a thin layer of 10km ($10^6 cm$) you need only a density of >$10^6 /cm^3$ of an element for the layer to become opaque in the line center. This is a very small density (a fraction $10^{-9} -10^{-6}$ of the hydrogen density in the lower solar atmosphere depending on the region) and most elements will easily exceed that (see the abundances in the plot in one of the other answers).

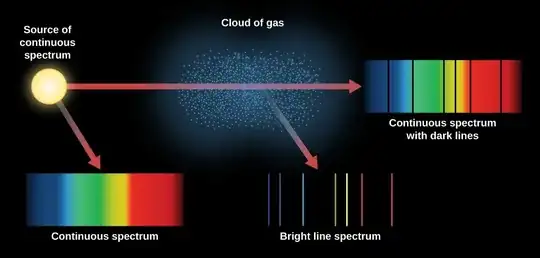absorption lines (from https://courses.lumenlearning.com/astronomy/chapter/formation-of-spectral-lines/)

EDIT (clarifying a couple of issues addressed in the comments below).

The illustration above can of course not be literally applied in case of the Fraunhofer lines in the solar spectrum. The 'cloud' is in this case a thin spherical shell around the sun, and, as we are observing from the outside, we are only able to see the spectrum with the lines in absorption. However, in principle we could see the other two cases if we could get below the layer; we would then see the lines in emission looking up and the featureless continuum looking down. The emission lines are being reflected back into the sun and are absorbed there (the photosphere can be considered a black body and thus absorbs any radiation falling onto it), so those photons disappear and can not be scattered back again into the absorption lines (as one of the comments was suggesting would be happening if one adopted this explanation).

The crucial point here is that the density of the chromosphere (where most of the Fraunhofer 'absorption' lines are formed) is much too low to be in thermal equilibrium. Atomic line emissions due to local thermal excitation by collisions can be neglected compared to the emission due to scattering of the photospheric radiation. As the chromosphere is nevertheless still optically thick within the lines, this results in the light being largely being scattered back into the photosphere at these frequencies, creating the 'absorption' lines in the process when viewing from the outside.

It also has been mentioned that the process at work here should be described as a separate absorption event followed by a spontaneous re-emission rather than a resonant scattering event (this is actually also implied in the link under the illustration above). Whilst this may seem like a subtle or even semantic issue, it is in fact quite important in some cases. The exact issue was actually already addressed 100 years ago in this paper and clearly suggested that the process that leads to the Fraunhofer lines should be considered as scattering (in the sense as described above) rather than an absorption/emission process. Whilst this paper used a classical approach, the same result is also obtained with Quantum Mechanics. This is derived in detail in §15 (Resonance Fluorescence) of the book 'The Quantum Theory of Radiation' by W. Heitler, which can be found on the Internet Archive. This proves that resonance scattering has to be described as a coherent one-quantum process. This means for instance that monochromatic radiation will again be scattered as monochromatic radiation and not with the natural line width of the transition (which one would see with a spontaneous emission).

This is in fact frequently applied in works regarding radiative transfer in spectral lines (in particular as far as stellar atmospheres are concerned) by incorporating 'partial frequency redistribution' functions that take the coherent nature of the scattering process into account. It is found that this can be crucial in some cases. This paper for instance shows that the observed polarization in the wings of strong Fraunhofer lines can only be explained with the coherent scattering model, with the incoherent 'spontaenous decay' model resulting in zero polarization in the line wings, in contradiction to observations.

Thomas
  • 3,061
  • 5
  • 12
  • I would have wrote "Absorption has a very large cross.." because Absorption/re-emission is certainly a resonance scattering process but the term can confuse new comers, absorption and emission are enough. This said, plus 1. – Alchimista Mar 22 '21 at 12:59
  • Resonance scattering is physically a completely different process compared to absorption/re-emission. The latter requires photoionization and subsequent recombination, whereas resonance scattering happens with the bound atomic electrons. Unlike absorption/re-emission it is a phase coherent process and scatters according to the Rayleigh-(Dipole) scattering phase function rather than isotropically. Anyway, I added now an illustration to describe qualitatively what is going on here. – Thomas Mar 24 '21 at 21:13
  • 1
    Absorption lines are due to absorption and spontaneous emission (at optical wavelengths) combined with a temperature gradient. Many absorption lines are "resonance lines" and do indeed have large cross-sections. The picture does not illustrate how absorption lines arise in the Sun, is misleading, and has lead to several other SE questions pointing out its flaws when applied to absorption lines from stars. – ProfRob Mar 25 '21 at 01:48
  • Exactly the debate I wanted to avoid. See also ProfRob comment. There is no need to describe absorption with more term, observation point of view. Also, whatever astrophysics, ionization, etc lines are due to absorption and spontaneous re-emission. No reason to call them resonance scattering, as I said. Because combining your answer and your last comment, it is you that must clarify to which process you refer to. – Alchimista Mar 25 '21 at 09:40
  • @ProfRob what is exactly wrong with the schematic? It seems that in a way it conveys what it should, namely lines are because there is a selective absorption of radiation. This said, I see that is very difficult to accept absorption for what it means. The answer is still confusing. – Alchimista Mar 25 '21 at 14:45
  • @Alchimista The Sun is not a light bulb on the other side of a cloud of gas. And if you put the light bulb in the gas there would be just as many photons scattered into the line of sight as out of the line of sight. – ProfRob Mar 25 '21 at 16:09
  • @ProfRob well apart the obvious fact that the sun isn't a bulb, it seems to depict the right principle. Unless I am totally wrong with the basic scheme that I've tried to explain to another user here https://astronomy.stackexchange.com/questions/41764/when-examining-an-exoplanets-atmosphere-is-the-stars-emission-spectra-or-plane. A bulb, for what it counts, surrounded by a gas, would certainly display a spectrum with missing absorption line (from the gas, if any abs takes place). – Alchimista Mar 25 '21 at 17:35
  • @Alchimista No it would not. In a spherically symmetric cloud there would be as many photons scattered into the line of sight as removed. Otherwise you have a conservation of energy problem, since in equilibrium there is just as much emission as absorption and there is nothing special about your line of sight. There must be a temperature gradient to get absorption lines. – ProfRob Mar 25 '21 at 18:42
  • @Alchimista Spectral lines are due to atomic resonances so by definition we are dealing with resonance scattering here (explaining the large cross section). And at least in the chromosphere, particle densities are much too small for collisions to disturb the scattering process (as given by the typical transition time of $10^{-8}$ sec). If you throw a ball against a wall and it reflects back into some given direction, would you then speak of absorption and emission? Hardly. Technically, you should speak of absorption only if the photon is completely destroyed e.g. in photoionization. – Thomas Mar 25 '21 at 21:39
  • @ProfRob Photons within the line are not conserved. Because of the Doppler effect they randomly change frequency and eventually migrate into the continuum where they can escape. So there is a constant loss of photons from the line that is not replaced by photons from the continuum (as continuum photons escape immediately from the sun anyway due to the small opacity outside the line). Furthermore, photons can be destroyed in regions of higher particle density when they excite an atomic transition which however is 'quenched' by collisions, so the photon can't be emitted again. – Thomas Mar 25 '21 at 21:40
  • This is plain wrong. The principle of detailed balance occurs for all processes microscopically, not just net effects. In a uniform temperature cloud, the Doppler profile is identical throughout and the effect you claim is non-existent. The only spectrum that an optically thick cloud (which the Sun is) at uniform temperature (which the Sun isn't) is a featureless blackbody spectrum. @Thomas – ProfRob Mar 25 '21 at 22:21
  • @ProfRob The solar atmosphere of the sun is not optically thick above the photosphere other than in the spectral lines. That's why you don't have a featureless blackbody spectrum. And an isothermal atmosphere will perfectly well produce these features (see also the line profile plots I showed in this respect in my reply at https://astronomy.stackexchange.com/questions/38862/problem-regarding-the-absorption-lines-of-the-sun/38870#38870 ; these are obtained through a full solution of the radiative transfer equation for a spectral line in an isothermal atmosphere). – Thomas Mar 25 '21 at 22:53
  • An isothermal atmosphere cannot produce spectral lines, as I demonstrated quite trivially in the same question. – ProfRob Mar 25 '21 at 23:57
  • 1
    Your radiative transfer simulation has a cold slab illuminated asymmetrically. This is like saying it is illuminated by a hotter layer! i e. A temperature gradient. Note also that this scenario isn't in thermal equilibrium and the slab cannot remain isothermal. This argument and your non-standard use of the term resonant scattering spoils a good answer. – ProfRob Mar 26 '21 at 00:11
  • Your argument about the photosphere is also wrong. A blackbody absorbs all radiation incident upon it and is in equilibrium at a single temperature. All blackbodies have a "surface layer" where they become optically thin. That is totally irrelevant to the emergent spectrum if everything is at the same temperature. In the solar photosphere it does matter but only because one sees to different depths that are at different temperatures. – ProfRob Mar 26 '21 at 00:21
  • Let us continue this discussion in chat. – ProfRob Mar 26 '21 at 00:24
  • @Thomas this is a brandly new (to me) definition of Electronic Absorption. If that is fine for you ok, I just warn readers. – Alchimista Mar 26 '21 at 10:03
  • @ProfRob gradient or no the symmetry is spherical anyway. I am dealing with the absorption line per sé. I don't get even the energy cons argument (though I could think on it). It could be for a gas omnidirectional illuminated, but I really don't get it for the line of sight direction joining observer (soectrophotomer) and star (source). This said, the acceptable answer by Thomas get worse and worse more comments are added. He managed to write something that does make sense based on misunderstood dictionary and principles, it seems. – Alchimista Mar 26 '21 at 10:08