I'm currently building an N-body simulator for my masters project and I'm using JPL's Horizons system to compare against.
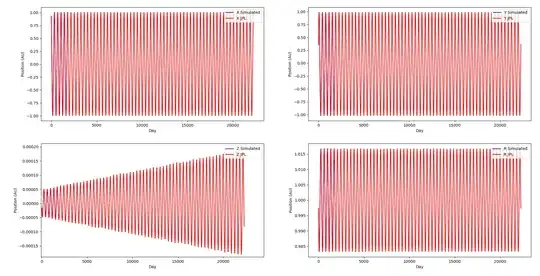
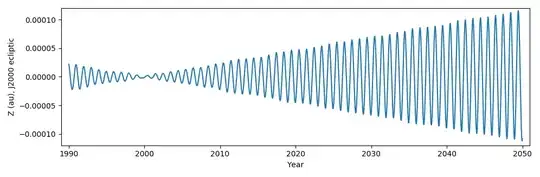
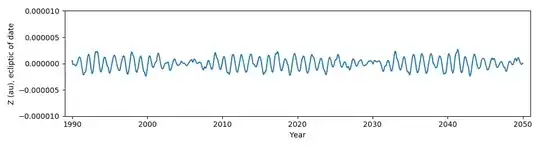
I started with just a couple orbits and everything seemed to be working nicely (After fixing many mistakes implementing a Fourth Order Integrator) but after extending to 10+ orbits I notice that in the Z-axis the Earth's amplitude increases linearly, according to JPL, but my simulation has a constant amplitude. JPL's result is shown in red in the bottom left:
What is causing this? Currently I only have the Sun, Earth, Moon and Jupiter in the system, but I didn't even realise the amplitude increased like this? What am I missing or got wrong?
(Also, the graph only shows 3 simulated orbits, and 80 JPL orbits)