A Sky Map of Gravity - what would it look like?

Question

PREAMBLE

Sky Maps exist which show the distribution and intensity of electromagnetic radiation received on Earth at various wavelengths. An obvious form is a map of the stars (Star Chart).

Maps have also been made for the distribution/intensity of Cosmic Microwave Background Radiation and "to visualize the X-ray Universe".

I find it interesting to consider the appearance of a Sky Map which showed the variation in intensity of the Gravitational Attraction Force (as currently experienced on Earth) attributable to masses lying in different directions (looking radially outwards from the Earth).

Essentially (if we start with a Newtonian Model) this would be a map which indicated the magnitude of the sum of "mass/distance_squared" for all the masses falling inside each particular pixel of the map. This then raises the questions of cosmological nature e.g. "how far do gravitational influences extend away from the Earth", along the lines of Olbers Paradox and "how was matter distributed through the Universe through time" - see The Cosmological Principle.

QUESTION

To bring this into the form of a question that can be answered succinctly, my question is: "What would a SkyMap of Radial Gravitational Force, looking outwards from Earth, look like (excluding that due to masses in the Solar System and Milky Way galaxy)."

APPENDIX

Calculation of Average Background Gravitational Force from Visible Universe

(Assuming, for simplicity, a static, spherical, universe of uniformly-distributed ordinary matter with Newtonian gravity and a test mass at the centre of the universe).

$\rho$ Average density of visible matter $=3*10^{-28} Kg/m^{3}$

$R$ Radius of visible universe $=1.7*10^{26} m$

Note:- values of $\rho$ and $R$ are obtained from here.

$G$ Universal Gravitational Constant $=6.673*10^{-11} Nm^{2}Kg^{-2}$

$f$ Fraction of sky represented by $3.6 * 3.6$ degree rectangular pixel $=1/(50*100)$ $= 0.0002$.

The formula for Force per unit mass $F_m$ is obtained by integrating (over the interval $0,R$) the incremental force per unit mass $F_i/m = G.M_i/R_i^2)$.

Here $M_i$ is the incremental mass contained within the incremental volume $V_i$ of the spherical shell of radius $R_i=R_{i-1}+\text{d}R$ and given by $M_i = \rho.V_i \approx \rho.4\pi.R_i^2.\text{d}R$.

Thus the total force/unit mass is given by:-

$$ F_m = G\int_0^R \frac{\rho.4\pi.R_i^2}{R_i^2}\text{d}R = 4\pi G \rho R $$.

And so the force per unit target mass per pixel is given by:-

$$F_{m,f} =4\pi G\rho R f = 0.86*10^{-14} NKg^{-1}.$$

Answer 1

The rough answer is: just like the sun makes it hard or impossible to see planets and stars during the day, it dominates the gravity sky.

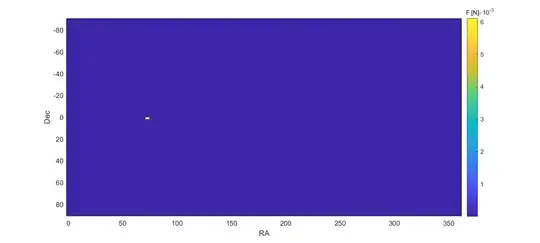
But there are interesting patterns there if we view the sky using a logarithmic scale.

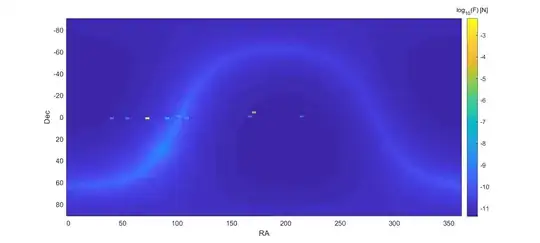
The above plots are a combination of the gravitational force of the sun, moon and planets, the stars in the Hipparchos catalog, the gravitational field of the Milky Way, and the nearby galaxies. Each component have a somewhat different effect.

The solar system

The force from the sun is shockingly big: 0.0059 N (per kilogram - I will omit that henceforth). At first this might appear impossible since we never notice the force, but remember that the setup for the question is a fixed point in space rather than the free-falling orbit of Earth. Because of the orbit this force exactly cancels.

Note that for spherical objects we only need to calculate the force from the direction of their centre of mass, not for their full extent. Hence regardless of what resolution I use for my map planets and stars will only change one box.

The force from the moon is $3.3198\cdot 10^{-5}$ N, a factor of 179 less. (Why do we experience tides from the moon more than from the sun? Because the gradient for the gravitational field is steeper for the nearby moon than for the remote sun). The other planets have much less effect, from $10^{-6.8}$ N for Jupiter down to $10^{-9.5}$ N for Neptune (and Pluto at $10^{-13.4}$).

For positions I used the Matlab Aerospace toolbox planetEphemeris function. Incidentally, I might well have messed up some of the many different coordinate frames here, so don't use these maps to navigate. The important thing for this question is the magnitudes of the forces anyway.

Stars

I added the field of the stars in the Hipparchos catalog, but they do not show up even on my logarithmic map because they are overpowered by the galaxy at large. If we just plot their contributions to different boxes we get the following map:

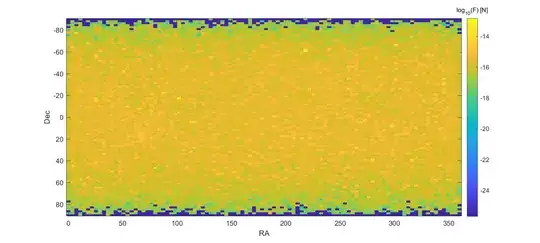
Note that the peak force in each box is on the order of $10^{-14}$ N: even Pluto matters more than nearby stars. This map also shows an annoying problem: if we just sum the contributions in each 3.6 times 3.6 degree rectangle in the coordinate system the polar rectangles will be narrow and have smaller area; hence there are fewer stars included and less force. Dividing by $\cos(\delta)$ removes this bias and shows that the stars indeed pull on us roughly equally in all directions.

(I used a rough estimate of their masses: assuming them all to be on the main sequence I calculated their luminosity from their absolute magnitude, and then estimated the mass as $M\approx M_\odot (L/L_\odot)^{1/3.5}$.)

The Milky Way

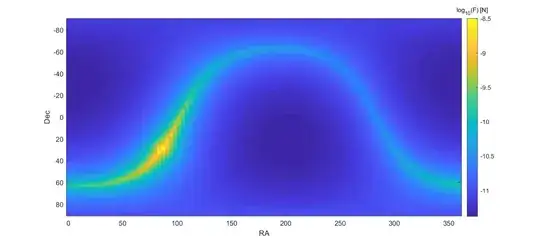
I modelled the Milky Way using the approximate values and formulas in Carroll & Ostlie (p. 884), essentially a neutral gas disk, a thin disk, a thick disk, a central bulge, a stellar halo plus a dark matter halo. The disks for example have density scaling as $$\rho(r,z)=\rho_0 e^{-r/h_r}e^{-|z|/h_z}$$ while the dark matter halo has the Navarro-Frenck-White profile $$\rho(r)=\frac{\rho_0}{\frac{r}{R_s}\left(1+\frac{r}{R_s}\right)^2}.$$ I integrate these functions along a ray extending from the part of the sky I am interested in. Note that the integral of the force will be $$F=\int_0^\infty \frac{G\rho(\mathbf{x}_0 + \mathbf{d} r)}{r^2} r^2 dr = G \int_0^\infty \rho(\mathbf{x}_0 + \mathbf{d} r) dr$$ since it is really an integral of an ever widening pyramid of area $r^2$: the total force is only dependent on the total amount of mass there. Since these density fields change slowly I ignore lateral variations. Again there should be a correction for declination, but it does not make a great difference in the picture.

The end result is a fair amount of force, especially along the galactic plane. This causes "galactic tides" in stellar orbits and can sometimes rival the force from remote planets in the solar system. Again, we do not notice most of the gravitational field because the sun is free-falling in the galaxy.

Sag A* does not show up in this image because it is not very massive compared to the full galaxy. The force is just $9.3678\cdot 10^{-15}$ N.

Nearby galaxies

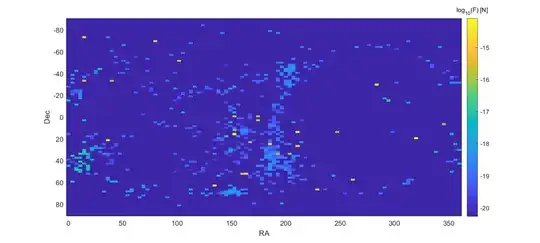
I used the NEARGALCAT catalogue to estimate the effect of nearby galaxies. This is in many ways the most dodgy estimate of all. While we know positions well we have weak data on actual masses. I used the estimated masses whenever they existed, and a linear fit between angular extent and mass derived from those to impute masses for galaxies lacking values. I am a bit uncertain if the mass estimates are just photometric or include dark matter; if not including DM, they should be an order of magnitude higher.

Typical forces are on the order of $10^{-19}$ N, although heavier galaxies might pull us with $10^{-15}$ N. They are hence on par with the nearby stars: totally overpowered by the galactic gravitational field and the solar system.

Technically, since galaxies are extended non-spherical objects, I should integrate over areas here. But there are limits to my energy.

In short, the gravity sky has nontrivial patterns if one has gravity-eyes with a logarithmic response.