My understanding is that a pulsar is a neutron star whose magnetic poles don't coincide with the rotational poles and whose magnetic poles sweep through Earth (allowing us to hear radio noise).
If we keep hearing pulsars, the polar offset must be very stable.
Why is such an alignment offset so stable?
The polar offset is not stable. Most researchers now think that the angle between the rotation axis and the magnetic field axis decreases with time. This is thanks to the same torquing mechanism which is slowing the pulsar down. The timescale on which this occurs is similar to the timescales on which pulsars lengthen their rotation periods to the point of switching off - i.e. of order 100,000 to a million years. Most of the (non-binary) pulsars that are observed are the remnants of a very recent supernova and there are probably a few hundred million "dead" pulsars in the Galaxy.
I guess if you mean stable on timescales of years, then yes they are stable. But over hundreds of thousands of years, they are not.
References:
Additional Details
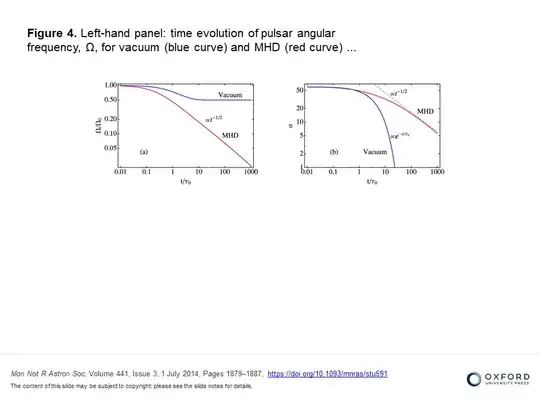
The picture below is from Philippov et al. (2014) and shows the time evolution of the rotation period of a pulsar and the the angle between magnetic and spin axes for a "vacuum" magnetosphere model and their favoured non-vacuum MHD magnetosphere - the time axis is in units of the initial pulsar spindown timescale.
Why is the timescale so "long"? Well, to align the two axes requires a very significant torque and change of angular momentum. As explained in Philippov et al. (2014), the alignment is caused by a component of the magnetospheric torque that acts upon the entire star, pulling the rotation and magnetic axes into alignment. The equation of motion for the angle of alignment $\alpha$ is $$\frac{d\alpha}{dt} = - \frac{K_x}{I\Omega}\ ,$$ where $K_x$ is the component of magnetospheric torque in the same plane as the rotation and magnetic axes, but at right angles to the rotation axis and $I\Omega$ is the angular momentum of the neutron star. Thus the instantaneous alignment timescale $\alpha/\dot{\alpha} \sim I\Omega/K_x$.
Since $K_x$ is just a component of the torque and $K_z$ (aligned with the rotation axis) is another, that causes the angular velocity to decrease on a timescale $I\Omega/K_z$, then the timescales for alignment and for pulsar spindown are of similar orders of magnitude (unless or until $\alpha$ becomes small, when the spindown torque vanishes). That spindown (and alignment) timescales are long in terms of a number of pulsar rotations is because $1/\dot{P}$ is a large number (typically $10^{14}-10^{16}$ rotations) for neutron stars - they have very large angular momenta compared with the torques acting upon them.
The magnetic field of a star is not entirely a result of the global spin of the star. The global spin is part of it, but there are other mechanisms as well. Within the star, there are convection zones, meridional flow, etc.
http://solarscience.msfc.nasa.gov/dynamo.shtml
All these flows generate their own field components. The overall field is simply the sum of all little fields. Its general orientation might be close to the global spin, if the strongest components are aligned to it, but there are many smaller components with different orientations. Therefore, the total field of the star can be somewhat slanted.
And then the star collapses into a neutron star, and its field is compressed. The collapse itself may be slightly asymmetrical, and may further deviate the magnetic field axis.
As a result of all of the above, it's by no means unusual that the magnetic field of the neutron star is not aligned with the spin.
