2

To find the best observation time for an object, I'd like to calculate the time when it is 30° or more above the horizon. Local Sideral Time would be sufficient.

To include that in my program, I need the formula.

Example: On June 4th, Jupiter has the coordinates RA= 9h 19m 28.0s Dekl= 16° 32' 0"

It rises at 10:32 and sets at 00:05.

After rise, when is it at altitude 30°, and after transit, when is it at altitude 30° again ?

I found this formula at http://www.stjarnhimlen.se/comp/riset.html. Although it's for the sun, it seems to be what I'm looking for.

$$\cos (\text{LHA}) = \frac{\sin (\text{h}) - \sin (\text{lat}) \times \sin (\text{Decl})}{\cos (\text{lat}) \times \cos (\text{Decl})}$$

Applied to the sample assuming a latitude of 45° I get.

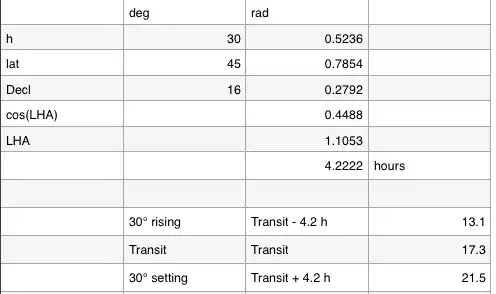
Sample caluclation
Is this the correct approach?

HDE 226868
  • 36,553
  • 3
  • 123
  • 201
ratlan
  • 121
  • 4
  • 1
    Check out catserver.ing.iac.es/staralt. – pela Jun 04 '15 at 09:01
  • Thanks, but I need the formula, not a tool. – ratlan Jun 04 '15 at 09:04
  • The earth rotates 15 degrees every hour. – andy256 Jun 04 '15 at 12:41
  • 15 degrees per hour: That's one part of the formula. – ratlan Jun 04 '15 at 12:52
  • I think you'd better explain what you know about the object(s) you want to observe. It's not at all clear what it is you don't understand. Given the coordinates of an object and the date, time, latitude and longitude, these are straight forward coordinate translations. – andy256 Jun 04 '15 at 12:59
  • @andy256 Thanks for your comment. I added an example to clarify my question. In the meantime I found a formula, but I'm not sure if I'm doing it right. – ratlan Jun 04 '15 at 15:12
  • An easy way to check your answer is to use Stellarium or http://ssd.jpl.nasa.gov/?horizons You may also want to look at my https://astronomy.stackexchange.com/questions/8390/cancelling-out-earth-rotation-speed-altazimuth-mount/8415#8415 (a closed form formula), but it's ugly. –  Jun 04 '15 at 15:24
  • @barrycarter Thanks. Comparing with Stellarium will not proove this is the correct approach. However if no one here neither posts an answer nor confirms the formula, I will test all relevant scenarios and hope for the best. The formula you mention would probably work, but as a non-mathematician I'm not able to bring d1 to the left side of the equation. Further the problem described requires two results. One when object rises, and one when it us about to set. In addition to that there are two special cases to be handled: 1)The object never gets below 30deg 2)The object never gets above 30deg. – ratlan Jun 05 '15 at 06:51
  • http://idlastro.gsfc.nasa.gov/ftp/pro/astro/hadec2altaz.pro confirms your answer is correct. The two special cases (always above 30 and never above 30) will occur when the right hand side is greater than 1 or less than -1, values the cosine can never reach (at least for real numbers) –  Jun 06 '15 at 03:44
  • You might want to look into PyEphem (if you're developing in Python) or its underpinning library libastro (if in C). http://rhodesmill.org/pyephem/ – Russell Borogove Jun 10 '15 at 23:46

3 Answers3

2

Yes, this is the correct approach. The $h$ in the equation is the altitude above the horizon of the object at which you consider it to be rising or setting. This is typically non-zero, because of atmospheric refraction, and, in the case of the Sun or the Moon, because of their finite diameters. In your case, the object 'rises' when it climbes above $h=30^\circ$ and 'sets' when it drops below that altitude.

If $\left|\cos(LHA)\right|>1$, there is no solution, because your object never crosses the $h=30^\circ$ line. $LHA$ is the local hour angle, and you can find the local sidereal time $\theta$ using

$LHA = \theta - \alpha,$

where $\alpha$ is the right ascension of your object.

AstroFloyd
  • 1,044
  • 6
  • 13
1

The answer is there on the stjarnhimlen.se site and also stargazing.net.

Now we can compute the Sun's altitude above the horizon:

sin(h) = sin(lat) * sin(Decl) + cos(lat) * cos(Decl) * cos(LHA)
LHA = LST - RA

h=Altitude=30$^\circ$, LHA = Local Hour Angle, lat= Your latitude on Earth, Decl = Object's declination, Ra = Object's right ascension, and LST = Local Standard Time. Just need to solve for LST.

eshaya
  • 3,706
  • 13
  • 31
0

You're not saying what programming language you're using. If it's Python, or if you could link Python libraries from it, then PyEphem would provide everything you need.

http://rhodesmill.org/pyephem/

Florin Andrei
  • 18,222
  • 2
  • 51
  • 67