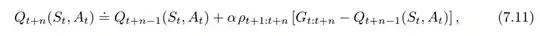6

In Sutton & Barto's book (2nd ed) page 149, there is the equation 7.11

enter image description here

I am having a hard time understanding this equation.

I would have thought that we should be moving $Q$ towards $G$, where $G$ would be corrected by importance sampling, but only $G$, not $G-Q$, therefore I would have thought that the correct equation would be of the form

$Q \leftarrow Q + \alpha (\rho G - Q)$

and not

$Q \leftarrow Q + \alpha \rho (G - Q)$

I don't get why the entire update is weighted by $\rho$ and not only the sampled return $G$.

nbro
  • 40,472
  • 12
  • 105
  • 192
Antoine Savine
  • 163
  • 4
  • Thank you @nbro for the edit, I was a bit lazy with the equations :) – Antoine Savine Apr 05 '19 at 14:30
  • Hi Antoine! Please, next time try to at least put some more effort to write these equations! Whenever I can, I try to write them nicely, but I would prefer if every user does it for its own questions/answers, of course! – nbro Apr 05 '19 at 14:31

2 Answers2

2

Multiplying the entire update by $\rho$ has the desirable property that experience affects $Q$ less when the behavior policy is unrelated to the target policy. In the extreme, if the trajectory taken has zero probability under the target policy, then $Q$ isn't updated at all, which is good. Alternatively, if only $G$ is scaled by $\rho$, taking zero probability trajectories would artificially drive $Q$ to zero.

Philip Raeisghasem
  • 2,056
  • 10
  • 30
  • This answer does show that the behavior is desirable but it's not a proof. How can one prove that this is the right thing to do? – Borun Chowdhury Jan 25 '24 at 23:45
  • In fact, we also need to realized that the importance sampling factor and the estimate are uncorrelated (I don't yet exactly understand why but in section 7.4 Sutton and Barto say "Notice that the control variate does not change the expected update; the importance sampling ratio has expected value one (Section 5.9) and is uncorrelated with the estimate, so the expected value of the control variate is zero." and the same reasoning would apply here) and since the importance sampling has expectation one, the two updates are equal on expectation. – Borun Chowdhury Jan 26 '24 at 00:19
0

This problem bothered me as well and I don't think the answer by Philip Raeisghasem above is satisfactory. Reducing variance is a desired property but one also has to show that the final result is correct.

Consider the general form of TD update

$$ Q_{t+n}(S_t,A_t) = Q_{t+n-1}(S_t,A_t) + \alpha \Delta $$

The desired property for $\Delta$ is that {\em under the behavior policy} $\mu$ we have

$$ \mathbb E_\mu[\Delta] = 0 $$

so that we have convergence under the behavior policy and that this expression makes sense for the problem.

Now consider

$$ \mathbb E_\mu[ \rho_{t+1:t+n} G_{t:t+n}] = \mathbb E_\pi[ G_{t:t+n}] $$

We also want to learn the state-action values for the target policy so we {\em would like}

$$ \mathbb E_\pi[ G_{t:t+n}] = \mathbb E_\pi[Q_{t+n-1}(S_t,A_t)] $$

However, under the behavior policy

$$ \mathbb E_\pi[Q_{t+n-1}(S_t,A_t)]= \mathbb E_\mu[ \rho_{t+1:t+n-1} Q_{t+n-1}](S_t,A_t)] $$

Extra steps of importance sampling do not affect the mean, and even though they increase variance, the resulting expression is often simpler. If we add an extra factor of $\rho_{t+n}$ to the expression for the state-action value we get the desired update rule using $$ \Delta = \rho_{t+1:t+n} ( G_{t:t+n} - Q_{t+n-1}) $$

Of course, there are modifications of this expression to removed importance sampling expression in the future of individual rewards in the return that are discussed in section 7.4 of Sutton and Barto.

Borun Chowdhury
  • 190
  • 1
  • 6