Funcție injectivă

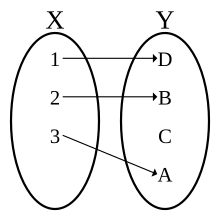
În această diagramă, componentele funcției pot fi listate astfel : 1D, 2B, 3A, C

O funcție ${\displaystyle f:A\rightarrow B}$ se numește injectivă dacă oricare ar fi ${\displaystyle x_{1},x_{2}\in A}$ două elemente ${\displaystyle x_{1}\neq x_{2}}$ diferite din domeniul de definiție atunci imaginile acestor elemente prin funcție sunt și ele diferite ${\displaystyle f(x_{1})\neq f(x_{2})}$.

O metodă de a stabili dacă o funcție este injectivă este testul liniei orizontale.

Definiție combinatorică

O funcție ${\displaystyle f:A\rightarrow B}$ se numește funcție injectivă (sau, simplu, injecție) dacă orice element din B este imaginea prin f a cel mult unui element din A.

În teoria speciilor, această definiție se scrie:

${\displaystyle \operatorname {Inj} (X,Y)=\operatorname {Ens} (X.Y+Y)}$

Pentru a afla direct din definiție numărul de funcții injective se trece la funcția generatoare exponențială:

${\displaystyle \operatorname {Inj} (x,y)=\exp(x.y+y)}$ ceea ce conduce la Șirul A008279 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)

Bibliografie

• François Bergeron, Gilbert Labelle, Pierre Leroux, Théorie des espèces et combinatoire des structures arborescentes, LaCIM, Montréal (1994). English version: Combinatorial Species and Tree-like Structures Arhivat în 2 octombrie 2006, la Wayback Machine., Cambridge University Press (1998).

Vezi și

• Definiție combinatorică
• Funcție surjectivă
• Funcție monotonă
• Funcție periodică