Poliedrul lui Steffen

În geometrie poliedrul lui Steffen este un poliedru flexibil descoperit în 1978[1]) de către Klaus Steffen și denumit după el. Se bazează pe octaedrul Bricard, dar, spre deosebire de aceste, nu se autointersectează.[2] Având 9 vârfuri, 21 de laturi și 14 fețe triunghiulare, este cel mai simplu poliedru flexibil care nu se autointersectează.[3] Fețele sale pot fi descompuse în trei subseturi: două pachete de șase triunghi dintr-un octaedru Bricard și încă două triunghiuri (cele două triunghiuri centrale ale desfășuratei prezentate în imagine) care leagă aceste pachete împreună.[4]

Poliedrul lui Steffen
Animație
Desfășurata. Liniile continui, respectiv punctate, reprezintă plieri „în munte”, respectiv „în vale”.

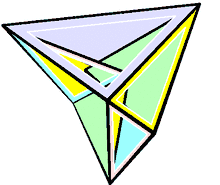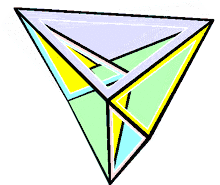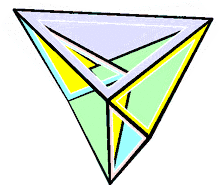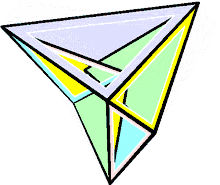
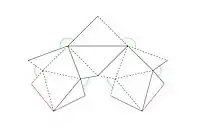
Se conformează teoremei tari a burdufului, ceea ce înseamnă că (la fel cu octaedrul Bricard, pe care se bazează) invariantul Dehn⁠(d) rămâne constant în timpul flexării.[5]

Note
  1. en Lijingjiao et al., Optimizing the Steffen flexible polyhedron, 2015
  2. en Connelly, Robert (), „Flexing surfaces”, În David A. Klarner, The Mathematical Gardner, Springer, pp. 79–89, doi:10.1007/978-1-4684-6686-7_10, ISBN 978-1-4684-6688-1
  3. en Demaine, Erik D.; O'Rourke, Joseph (), „23.2 Flexible polyhedra”, Geometric Folding Algorithms, Cambridge University Press, Cambridge, pp. 345–348, doi:10.1017/CBO9780511735172, ISBN 978-0-521-85757-4, MR 2354878
  4. en Fuchs, Dmitry; Tabachnikov, Serge (), Mathematical Omnibus: Thirty lectures on classic mathematics, Providence, RI: American Mathematical Society, p. 354, doi:10.1090/mbk/046, ISBN 978-0-8218-4316-1, MR 2350979
  5. en Alexandrov, Victor (), „The Dehn invariants of the Bricard octahedra”, Journal of Geometry, 99 (1-2): 1–13, arXiv:0901.2989 Accesibil gratuit, doi:10.1007/s00022-011-0061-7, MR 2823098

Legături externe
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.