Morfism de grupuri

În matematică, o funcție $f:G\rightarrow G'$ se numește morfism de grupuri în următoarele condiții: $G\ {\text{si}}\ G'$ admit fiecare o structură de grup, cu operațiile notate $\cdot$ și respectiv $\circ$ , iar

f(x\cdot y)=f(x)\circ f(y)\quad ,\forall x,y\in G

Proprietăți

Dacă e și e' sunt elementele neutre ale lui G si G' atunci f(e)=e'.
$\forall$ x $\in$ G, $f(x^{-1})=(f(x))^{-1}$ .
θ : G → G', θ(x)=e', x $\in$ G este evident morfism de grupuri numit morfismul nul.
Compunerea de morfisme de grupuri este tot un morfism de grupuri.
1_G : G → G, 1_G(x) = x, x $\in$ G este evident morfism de grupuri numit morfismul identic al grupului G. În plus, dacă f : G → G' este morfism de grupuri atunci au loc: f ∘ 1_G = f și 1_G' ∘ f = f.
f este izomorfism de grupuri dacă și numai dacă f este bijectivă.

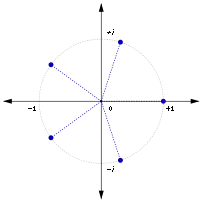
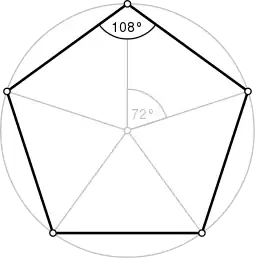
Izomorfism între grupul multiplicativ al rădăcinilor de ordin cinci ale unității și grupul rotațiilor pentagonului echilateral

Vezi și

Izomorfism

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.