Concoida lui de Sluze

Curbele sunt definite de ecuația în coordonate polare[3]

${\displaystyle r=\sec \theta +a\cos \theta .}$

În coordonate carteziene curbele satisfac ecuația implicită^⁠(d)[3]

${\displaystyle (x-1)(x^{2}+y^{2})=ax^{2}\,}$

cu excepția cazului a = 0, forma implicită are un punct izolat în (0,0), care nu este prezent în forma polară.

În formă parametrică pot fi scrise sub forma[3]

${\displaystyle x=(\sec t+a\cos t)\cos t}$

${\displaystyle y=(\sec t+a\cos t)\sin t}$

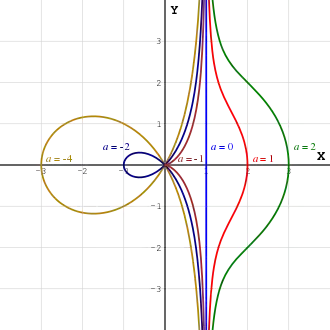
Sunt curbe raționale^⁠(d), circulare, cubice^⁠(d).

Aceste expresii au pentru a ≠ 0 o asimptotă x = 1. Punctul cel mai îndepărtat de asimptotă este (1 + a, 0). Pentru a < −1 (0,0) este un nod.

Pentru a ≥ −1 aria dintre curbă și asimptotă este

${\displaystyle |a|(1+a/4)\pi \,}$

în timp ce pentru a < −1 aria este

${\displaystyle \left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}-a\left(2+{\frac {a}{2}}\right)\arcsin {\frac {1}{\sqrt {-a}}}.}$

Dacă a < −1, curba va avea o buclă. Aria buclei este

${\displaystyle \left(2+{\frac {a}{2}}\right)a\arccos {\frac {1}{\sqrt {-a}}}+\left(1-{\frac {a}{2}}\right){\sqrt {-(a+1)}}.}$

Patru dintre curbe au nume proprii:

• a = 0, dreaptă (asimptota restului curbelor din familie);
• a = −1, cisoida lui Diocles^⁠(d);
• a = −2, strofoida^⁠(d) dreaptă;
• a = −4, trisectoarea lui Maclaurin

Asemănătoare cu concoida lui de Sluze este concoida lui Nicomede, a cărei ecuație în coordonate polare este:[4]

${\displaystyle r=a\sec \theta +b.}$

• en Curves: Conchoid of de Sluze la MacTutor