Compus de patru octaedre

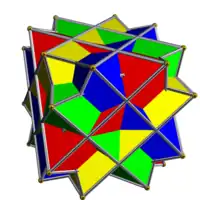
În geometrie compusul de patru octaedre este un compus poliedric uniform realizat dintr-un aranjament simetric de 4 octaedre, considerate ca antiprisme triunghiulare.[3]

Descriere
Compus de patru octaedre

(model 3D)
Tip	compus poliedric uniform UC₁₁ - UC₁₂ - UC₁₃
Fețe	32 triunghiuri echilaterale
Laturi (muchii)	48
Vârfuri	24
Configurația vârfului	3.3.3.3[1]
Configurația feței	V4.4.4
Diagramă Coxeter	[5{3,4}]2{3,5}[2]
Grup de simetrie	Compus: octaedrică (O_h) Constituenți: antiprismatică (D_3d)
Arie	≈4,889 $a$ ² ( $a$ = latura)
Volum	≈1,886 $a$ ³ ( $a$ = latura)
Poliedru dual	compus de patru cuburi
Proprietăți	Constituenți: 4 octaedre
Figura vârfului

Are indicele de compus uniform UC₁₂.[3]

Construcție

Poate fi construit prin suprapunerea a patru octaedre identicce și apoi rotirea fiecăruia cu un unghi egal, de 60°, în jurul unei axe separate care trec prin centrele a câte două fețe opuse ale octaedrului. Are simetrie octaedrică, (O_h). Anvelopa sa convexă este un cub trunchiat neuniform. Dualul său este compusul de patru cuburi.

Mărimi asociate

Coordonate carteziene

Coordonatele carteziene ale vârfurilor compusului sunt permutările lui

(\,\pm 2,\,\pm 1,\,\pm 2\,)

Arie

Următoarea formulă pentru arie, $A$ este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) $a$ :[4]

{\frac {494}{175}}{\sqrt {3}}\,a^{2}\approx 4,889332

.

Volum

Următoarea formulă pentru volum $V$ este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) $a$ :

V={\frac {4{\sqrt {2}}}{3}}\,a^{3}\approx 1,885618~a^{3}.

Note

sno, bendwavy.org, accesat 2023-08-18
en H.S.M. Coxeter, Regular polytopes, Methuen & Co. Ltd., 1948, pp. 49–50, 98
en Skilling, John (1976), „Uniform Compounds of Uniform Polyhedra”, Mathematical Proceedings of the Cambridge Philosophical Society, 79 (03): 447–457, doi:10.1017/S0305004100052440, MR 0397554
en Eric W. Weisstein, Octahedron 4-Compound la MathWorld.

Vezi și

Lista compușilor poliedrici uniformi

Compuși de octaedre

Legături externe

en Klitzing, Richard. „3D compound”.
en model VRML
en Polyhedron Category C9: Octahedral Continuums Sno

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[bw-1] sno, bendwavy.org, accesat 2023-08-18

[2] H.S.M. Coxeter, Regular polytopes, Methuen & Co. Ltd., 1948, pp. 49–50, 98

[S-3] Skilling, John (1976), „Uniform Compounds of Uniform Polyhedra”, Mathematical Proceedings of the Cambridge Philosophical Society, 79 (03): 447–457, doi:10.1017/S0305004100052440, MR 0397554

[SW-4] Eric W. Weisstein, Octahedron 4-Compound la MathWorld.