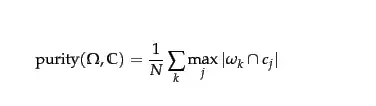24

In cluster analysis how do we calculate purity? What's the equation?

I'm not looking for a code to do it for me.

enter image description here

Let $\omega_k$ be cluster k, and $c_j$ be class j.

So is purity practically accuracy? it looks like were summing the amount of truly classified class per cluster over the sample size.

equation source

The question is what is the relationship between the output and the input?

If there's Truly Positive(TP), Truly Negative (TN), Falsely Positive(FP), Falsely Negative (FN). Is it $Purity = \frac{TP_K}{(TP+TN+FP+FN)}$?

Iancovici
  • 795
  • 2
  • 5
  • 17
  • 3
    If you just need a quick definition: The top google search on clustering purity ** links here which gives a mathematical definition. (** for me, at least -- your individual results may differ) – Glen_b Apr 29 '14 at 23:55
  • In classification trees some of the functions to measure impurity are: resubstitution error, gini-index and entropy. (Classification trees perform a specific form of clustering, so I think this should be relevant.) Hope this helps! – Angelorf Apr 30 '14 at 10:24
  • I have no idea what you mean by 'purity', but David Colquhoun uses "the black magical assay of purity of heart" as an example of binomial sampling on pp. 111-114 of his excellent textbook Lectures on Biostatistics (1971) which is available as a free pdf from the author's website: http://www.dcscience.net Even if it is irrelevant to your question, it's a great story. – Michael Lew Apr 30 '14 at 02:02

1 Answers1

35

Within the context of cluster analysis, Purity is an external evaluation criterion of cluster quality. It is the percent of the total number of objects(data points) that were classified correctly, in the unit range [0..1].

$$Purity = \frac 1 N \sum_{i=1}^k max_j | c_i \cap t_j | $$

where $N$ = number of objects(data points), $k$ = number of clusters, $c_i$ is a cluster in $C$, and $t_j$ is the classification which has the max count for cluster $c_i$

When we say "correctly" that implies that each cluster $c_i$ has identified a group of objects as the same class that the ground truth has indicated. We use the ground truth classification $t_i$ of those objects as the measure of assignment correctness, however to do so we must know which cluster $c_i$ maps to which ground truth classification $t_i$. If it were 100% accurate then each $c_i$ would map to exactly 1 $t_i$, but in reality our $c_i$ contains some points whose ground truth classified them as several other classifications. Naturally then we can see that the highest clustering quality will be obtained by using the $c_i$ to $t_i$ mapping which has the most number of correct classifications i.e. $c_i \cap t_i$. That is where the the $max$ comes from in the equation.

To calculate Purity first create your confusion matrix This can be done by looping through each cluster $c_i$ and counting how many objects were classified as each class $t_i$.

   |  T1 |  T2  |  T3
---------------------
C1 |  0  |  53  |  10
C2 |  0  |  1   |  60
C3 |  0  |  16  |  0

Then for each cluster $c_i$, select the maximum value from its row, sum them together and finally divide by the total number of data points.

Purity = (53 + 60 + 16) / 140 = 0.92142
joelgenter
  • 3
Snives
  • 506
  • can you also please answer for entropy? – Furkan Gözükara Mar 01 '16 at 11:50
  • here my question : http://stackoverflow.com/questions/35709562/how-to-calculate-clustering-entropy-a-working-example-or-software-code/35716423 – Furkan Gözükara Mar 01 '16 at 11:51
  • I think you "overflow the logic" when say "$t_j$ is the classification ... max counts". There is no need for $max_{j}$ then. By the way, high purity does not shows the correctness of classification, does it? – LRDPRDX Nov 20 '17 at 17:57