I am teaching those topics (arithmetic/geometric series) just now, and want some not so standard (fun) examples, which can be used essentially at high school/beginning calculus level. I'm considering some, and will post them as answers, but first I'll wait to see what others can come up with.
With standard examples of geometric series, for instance, I think about applications to interest/loan/annuity calculations, and so on.
Here's one you've probably seen. But I'll post it since I like it a lot.
$\sum_{k=0}^{\infty}(1/\phi^2)^k=\phi$
where $\phi$ is the golden mean $1+(\sqrt{5}-1)/2$, approximately 1.618
The classic examples of the first $n$ natural numbers, first $n$ even numbers, and first $n$ odd numbers are all nice introductions. Here are some pictures I created to help explain them using blocks:
Natural numbers:
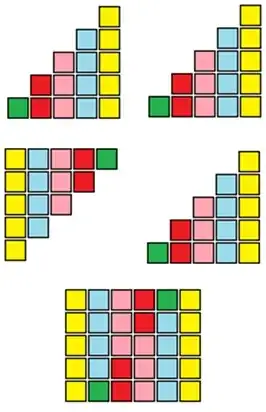
Even numbers:
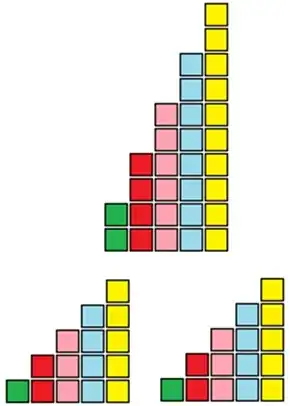
Odd numbers:
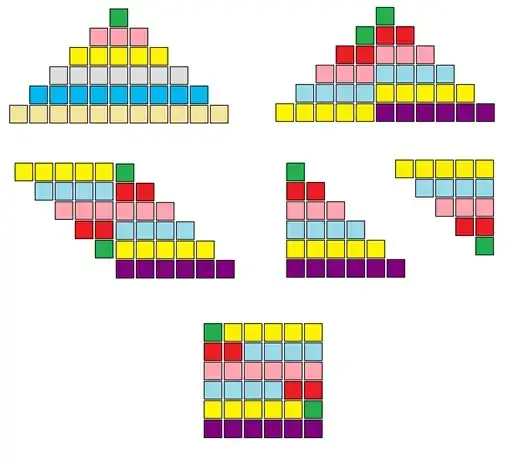
Similar to the binary example given earlier, here is one using ternary (base 3):
$$0.020202\ldots = \sum_{n = 1}^{\infty} \frac{2}{3^{2n}} = \sum_{n = 1}^{\infty} \frac{2}{9^n} = \frac{1}{4}$$
Though the question concerns the beginning Calculus level, those later in their mathematical learning may note that the line above indicates $1/4$ is in the Cantor set.
Since you asked for nonstandard: Rarely have I seen these problems asked in reverse. For example, Given a natural number $k$, what's an algorithm that could be used to determine if there is some $n$ such that the sum of $1, 2, \ldots, n$ gives $k$?
Does this approach work? Suppose you are given $666$. The sum of $1, 2, \ldots, n$ is $n(n+1)/2$, so we now ask whether there is an $n$ for which $2\cdot 666 = n(n+1)$. Taking the square root of the left side, we find $\sqrt{2\cdot 666} = 36.49657\ldots$, which suggests checking $n = 36$. (And it works!)
Similarly, suppose you are given $902$. Reasoning as above, we find $\sqrt{2\cdot 902} = 42.47352\ldots$, which suggests checking $n = 42$. (But no: $42(43)/2 = 903$. A narrow miss!)
One more: If you will allow for modifications similar to the $41 + \sum_{k=0}^{n}2k$ example, then consider:
$$23 + \sum_{k=0}^{n}6k$$
Observe that this can be re-written as $3n^2 + 3n + 23$, which is prime for $0 \leq n \leq 21$.
A nice follow-up problem is to prove that there cannot be a real-valued polynomial producing primes when evaluated at every natural number.
As an engineering student, I dealt with binary all the time. A good calculator would convert from decimal to binary, hex, octal. When converting 1/3 to binary, I noted that it's .01010101... Which if you are used to reading binary past the decimal point is simply 1/4+1/16+1/64.... This seemed interesting to me.
I like
$41+\sum_{k=0}^{0}2k$,
$41+\sum_{k=0}^{1}2k$,
$41+\sum_{k=0}^{2}2k$,
… through
$41+\sum_{k=0}^{40}2k$
Each sums to a prime except for the 41st sum which is $41^2$
Attached is a pic of this sequence of primes:
Good answers!! What I had in mind was this:
Fractals, as the Koch snowflake: https://en.wikipedia.org/wiki/Koch_snowflake
The area is a convergent geometric series, while the circumference is infinite, represented by a divergent geometric series. The geometric series arises in such problems because of the self-similarity of the figure.
This might be a bit ambitious but you could describe how the geometric series enters the Euler Product Formula for the Euler-Riemann zeta function (you could just introduce this as a real-variable function and handle the products formally).
How about arithmetico-geometric series? I.e., a series of the form $$ \sum_{n=1}^\infty P(n) a^n $$ where $P(n)$ is a polynomial and $a\in \mathbb{R}$ is the ratio of the series. For example, find $$ \sum_{n=1}^\infty n \left(\tfrac12\right)^{n+1}. $$ A proof-without-words and one with words (although they're in Spanish) can be found here.
If you're looking for examples you can show to students without any background in computer science, consider the following:
For geometric series, family trees. Each person has two parents, and each parent has two parents, and each grandparent also has two parents, and so on. This is an example of sums of powers of two, which is a geometric series.
For arithmetic series, acceleration. Every second, the number of centimetres per second an object moves increases by a constant amount.
